Site Index
• Wiki
• Blog
February 2022, AM writes:
"Very cool page on the Sharp EL-5500III! I have one and I absolutely love it."
December 2014, AV writes:
"I am very impressed with your
credentials and interests. I began using my EL5500III again after about
twenty years. It's amazing how much of the programming I still
remember. While looking for a manual online, I luckily came upon your
site. Incredible. I might even try to build your analog upload system.
I use my Sharp to program CNC
machines, mostly WEDM (wire electrical discharge machining) in shops
where there is an absence of CAD assistance. I never had a way to back
up. I sold one of my first programs to a guy working on space shuttle
parts or something for Moog back in '86 in Pinellas Park Florida. I
think I got around $75.00 for it.
Anyways, Great site!"
Introduction
This page documents calculators that "Do Something More!" or are
special in some way. Currently, HP-20S, Sharp EL-5500III,
and Sharp EL-5500II.
HP-20S:
Installing ROM Programs into RAM
The
HP20 HP-20S runs on 4 "hearing aid" batteries (Alkaline LR44, AG13,
A76, or Silver Oxide SR44, 303, 357). It has many
functions pre-associated with key strokes on the
keyboard. It has a funky 2 number stack where Y is visible in the
display and SWAPs with X hidden in a non-visible location. Mostly
it's alebraic operations except when the funky stack is used to do %CHG
calcs, polar/cartesian conversions, stats combination and permutation
calculations.
There are also six programs that you can download from
internal ROM memory into the calculators executable RAM memory. You can view
a quick documentation here on the web page, or download a ROM spreadsheet that
documents the
programs. The spreadsheet is much more detailed. The six
programs are...
ROM A - Root
finder
ROM B - Integrator
ROM C - Complex Number Math
ROM D - 3x3 Matrix Math
ROM E - Quadratic Equation Root finder (specific case of Root finder)
ROM F - Regression fit to power, exponential, and log functions
In case you forget how to quickly access and use the ROM programs, you
can download a ROM Cheat
sheet
to carry with
you.
GOTO {letter|digit} goes to
that program label and does not execute the label step.
Left V shows the next program
step to execute, which executes when you release the V key.
XEQ {letter|digit} goes to that
lable and starts executing until R/S instruction
HP20-S
Screen/keyboard repair
Here are more details how to use each ROM program.
Find roots - ROM A
PRGM LOAD A SHOW PRGRM
(checksum BC6C)
PRGM ^ (so you see the LBL F 62
- 61 41 F), then key in your function. You can use memory
locations 0 through 4 (the program used 5-9). Terminating with
RTN is optional because it's assumed after the last instruction. Exit programming with PRGM.
Make sure you're in DEC mode because HEX or OCT or BIN don't do
fractions.
To find one root (where the function crosses the X-axes, evaluating to zero), enter an intial quess for x and press XEQ A.
Try again with other
initial guesses to find all the roots. Periodic functions may
have many zeros and you'll find the one your guess is "sloped toward"
to start. By default the program does a max of 100 interations
before giving up. Defaults can be changed (see the spreadsheet
referenced above).
Here's a fun example of finding roots. For a road trip, is it cheaper to drive a camper
and accept lower gas mileage ($0.17/mile) in order to have no hotel
costs, or should you just pay the hotel costs and drive a tiny fuel
efficient car ($0.06/mile) ? If you drive LOTS of miles in a day, it's
clearly cheaper to take the fuel efficient car. But if you're poking
around doing sightseeing and drive only a few miles each day, it's
cheaper to take the camper. How many miles per day is the breakeven
point? Set the two costs equal and solve for a zero on one side:
camper cost = car cost
m * 0.17 = m * 0.06 + 80
(0.17m) - (0.06m+80) = 0
I know it's also easy to symbolically solve for m in this case,
but imagine if both equations were very complicated with trig functions
and log functions and lots more. The calculator can find zeros
even when you can't analytically solve the formulas. Be careful
of functions that "blow up" such log(zero) and things like that. If you
look at the spreadsheet, I show at least one work around - checking for
bad cases and substituting an "almost infinity" answer.
Put the equation into the program at LBL F
GTO F PRGM = STO 0 * .17 - RCL 0 * .06 - 80 = PRGM
Enter a guess and find the answer. 100 XEQ A
727 miles.
|
Integrate functions - ROM B
Pending
Complex Math - ROM C
pending
3x3 Matrix Math - ROM D
pending
Quadratic Equation Root
Finder - ROM E
pending
Fit power, exponential, or log data
- ROM F
PRGM LOAD F SHOW PRGM (checksum
8641)
Clear statistical data with CLRG
XEQ A to choose power (y=bxm), XEQ B to choose exponential (y=bemx), XEQ C to choose logarithmic (y=mln(x)+b).
Enter data as X INPUT Y R/S,
repeatedly for all data pairs, display shows you how many you've
entered so far. Remove data with X
INPUT Y XEQ 9
Y XEQ D gives expectation value for X, and r-fit value (r=1
perfect fit).
X XEQ E gives expectation value
for Y, and r-fit value (r=1 perfect fit).
XEQ F gives slope and
intercept. For exponential data, the calculator native stats function
reports (m,b') to make ln(y)=mx+b' true, but the program reports b=
exp(b') so that y=b*exp(mx).
For logarithmic data, calculator native stats function reports (m,b) to
make y=m*ln(x)+b, and the
program reports the same (m,b). For power data, the calculator
stats function reports (m,b') to make y=mln(x)+b' true, but the
program reports (m,b) so that y=bxm.
Internally, this program simply pre-compensates all the data going into
the stats route. For power, BOTH are converted so that the
calculator internally
uses ln(x), ln(y) data. So, don't try to put the data point (0,0)
into
the computer. For exponential data, the y value is converted to ln(y) which now makes
the data linear; so don't enter (x,0) as data. For logarithmic data, the x is converted to ln(x), which is linear if y
was logarithmic; don't enter data (0,y).
Sharp EL-5500II
EL5500III: Listing and Saving Programs
The Sharp EL-5500II and Sharp EL-5500III handheld
calculators came from on era when people used the
TRS-80 computers programmed in BASIC, and the HP-41 and TI-83
introduced programmability into the calculator market.
The EL-5500s combined a standard calculator on the right side of the
keypad with a QWERTY-like keypad for using a BASIC interpreter
programmed into the calculator. Rather than writing cryptic
pneumonic programs with a TI or HP calculator, you could program
directly in the BASIC language.
True to other computers of the time, programs were saved on audio
cassette tape output of the EL-5500iii.
Use the BASIC
command line CSAVE or "CS." for short.
The computer has no battery backup when you replace the main two
batteries, so
be sure to save all your BASIC programs before changing
batteries. That said, you won't be changing batteries that
often. The two CR2032 batteries last between 10 and 20
years. Buying a pack of 10 CR2032 batteries cost me a whopping $2.19
on eBay. I think that works out to about 75 years of
operation.
Eddie Shore has documented a number of programs to run
on this computer. He links two of his own pages and pages of
others:
Eddie
Jan 2017
Eddie
May 2018
Music
YouTube video
Matrix
Ops #1
Matrix
Ops #2
With the LLIST or "LL." command, the Sharp computer will send programs
out the port without modulation. Originally, this function was
designed to print onto their printer. I suspect it's
ASCII-like and for greater compatibility should be inverted to ±12
volts to match RS-232.
With LLIST there is some handshaking involved. In order to get
the EL-5500III to send data, you have to hold one of the inputs
high. That's what I was doing with the 10 Kohm resister in the
picture. I have more work to do in order to
document this in detail.
When using the audio function, audio output of the modem is a square
wave output, with modem
frequencies of
4000 Hz and 2000 Hz. Bit time is about 2 milliseconds and signal is 4
volts peak-to-peak.
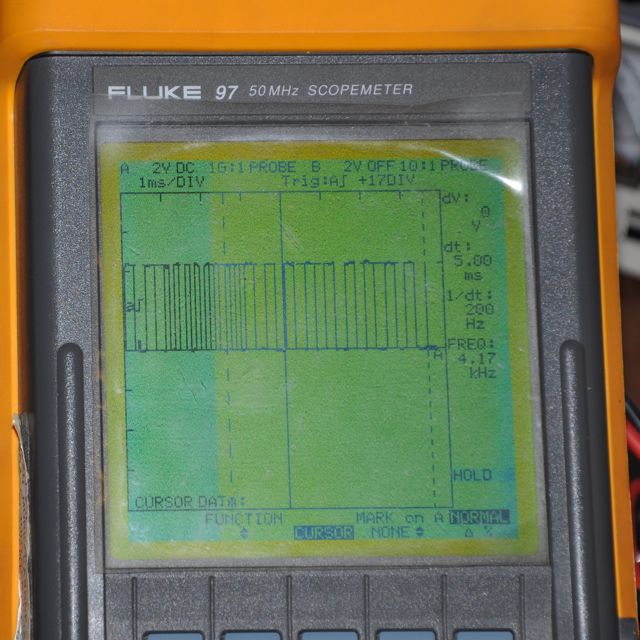
Saving EL-5500 BASIC programs as audio files on your PC
computer
Contrasting the LLIST function, the modulated audio waveform from
CSAVE was meant to record data or programs on a
cassette tape. This was pretty normal back in
the
late 1970s and 1980s. My first experience with this was with a
Texas Instruments Sinclair computer. Thirty years later, it
seemed appropriate to see if I
could record the audio on my laptop computer and save/restore
programs as mp3
or wav files.
Below is a picture of the setup I used. The ancient laptop peeking over
the top of the Macbook is not used. On the left is a Fluke 97
digital
scope. Next the Macbook, then a perfboard electrical prototyping
board, then the EL-5500. Notice the audio wire from the perfboard
wraps around behind the Macbook laptop and plugs into the audio port of
the laptop. The o'scope wires go behind the laptop and come out
to the perfboard area.
It appears Sharp is sort of like the old
U.S. Navy electronics courses. They recognize that electricity is
made up from negatively charged electrons, so when you read
documentation on this 11-pin interface, remember "GND" (pin 2) is at 5
volts and "Vcc" (pin 3) is ground. The green ground wire plugged
into the
3rd hole from the top. The cassette tape audio output
is on the
7th hole from the top. I routed the audio voltage across a 10
kohm
resistor potentiometer with a center tap for a volume adjust. The
Sharp has no trouble with a 10 kohm load, and the laptop audio standard
has a high input impedance so it also doesn't load the circuit.
Turns out a volume of about 1/3 scale on the potentiometer worked fine.
Here's a zoomed in view of the I/O connector.
The two wires from the potentiometer to the laptop computer needed to
convert to a 1/8 phone plug. I had an extra stereo headset wire
left over. Wow! Those wires are really small shielded
cables. The connections were so fragile I got out a glue gun and
added a cardboard splint on the connection.
The Macbook needed to be told to use it's audio port as an input rather
than a headset output. Use the sound option in the System
Preferences app as shown below. Your computer may not have the
Soundflower entries. Soundflower is a separate program I found
that lets me route audio from any application to any other application,
but it's not used to record the EL-5500 cassette audio.
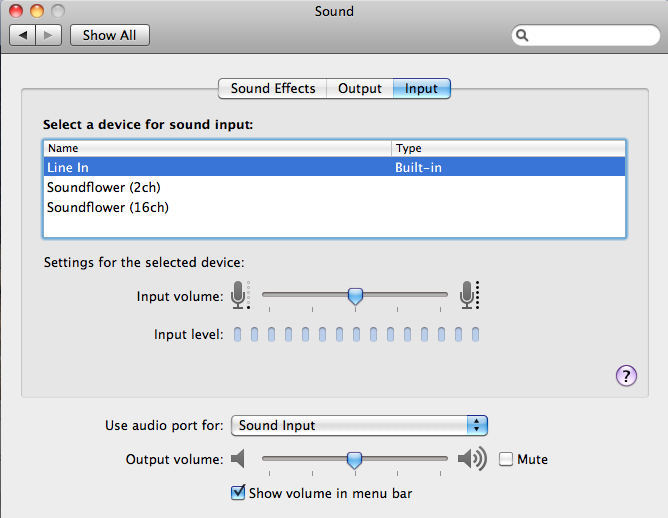
You can use Quicktime to record the audio, but I prefer to use
Audacity, which is kind of like GIMP for audio files. I entered
CSAVE into
the EL-5500 and below the audio that was recorded. The part shown
below is where the lead-in 4000 Hz carrier is FSK to 2000 Hz for bit
times of
2 mSec.
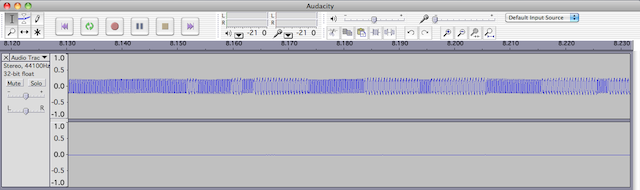
On the above Audacity screen capture, you can see only a section of the
full
audio. You can download the full audio here (160
KB mp3 1.7
MB wav).
Be ready for a long screeching lead in tone, and then a very quick
burst of modulation at the end that represents the program below.
The modulated part is very short because the program listing is only 5
lines
long, totaling 66 characters, counting the spaces and a CR on each
line. For later analysis below, I trimmed off the leading 8.008
seconds and normalized peak amplitude to -9dB using Audacity.
Here is the BASIC program that was saved out the cassette audio port
with the CSAVE command, so the audio file is actually a rendition of
this program. Now I need to figure out a way to play this audio
file back to the calculator so I can reload programs and data onto it.
10 INPUT A
20 FOR I=A TO 0 STEP -1
30 PAUSE I
40 NEXT I
50 BEEP A
|
The oscilloscope and Audacity showed a Mark tone of 4000 Hz and a Space
tone of 2000 Hz and
bit time of 2 ms (500 bps). The linux "file" command confirms a
sample rate of 44100 Hz. Using a different Linux program (sox), the
exported wav file was converted from stereo to monotone and I
trimmed off 7 seconds of the lead-in tone. For the spectrogram I
skipped the first 1.1 seconds of the shortened file and showed only 1.6
seconds before the carrier drops away.
sox stereo.wav mono.wav remix -
sox mono.wav monoshort.wav trim 7
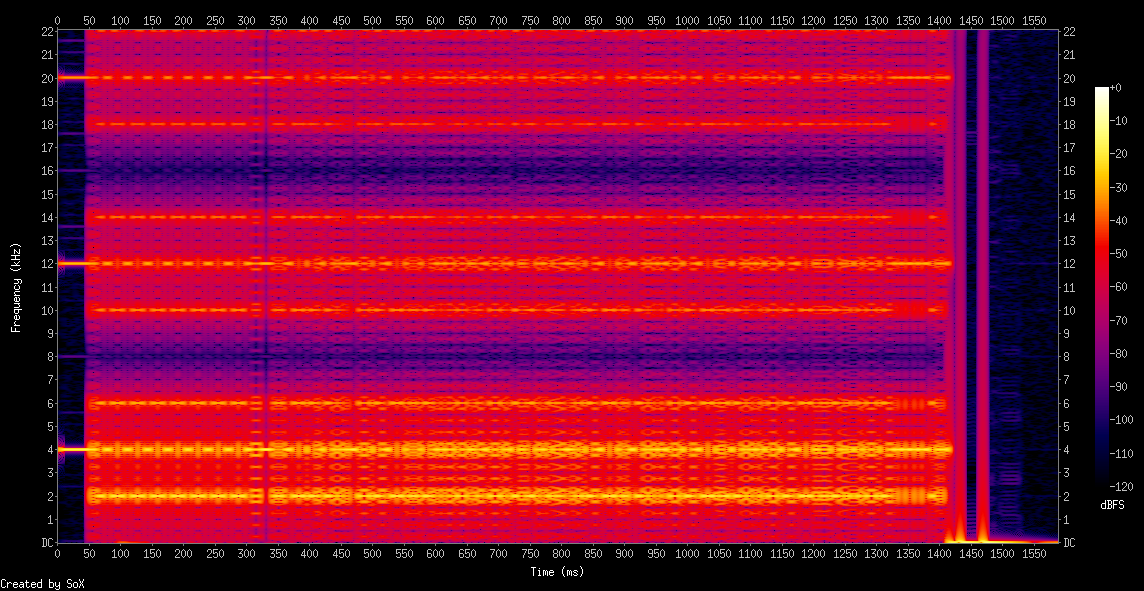
You can also see a spectogram of the audio file using sox:
sox monoshort.wav -n trim 1.1 1.6 spectrogram -x 1000 -o spectrum.png
Notice the significant overtone signals due to the square wave
shape of
the audio recorded. You can also see this zooming in with
Audacity or looking at the Octave plot. Overtones are at 12 kHz
and 20kHz.
I have also analyzed the data using Octave (Matlab clone). Here's
a picture of the data row vector from Octave.
% Octave script
data = audioread("monoshort8008n9.wav");
plot( data )
axis([6250 7500]);
disp("Done. Look for plot in a separate window");
Guessing at asynchronous protocols
The spectrogram and
Audacity shows a lead-in data pattern that repeats every 16 bit
times.
Maybe there are 8-bit bytes (including the start
bits). Using another Linux utility shows the digital data
including
the start bits, and then shows the solid sequence of "1"s for the
4000KHz lead-in tone, then bits including possible "0" start
bits.
root@kali:~# minimodem --rx -R 44100 --mark 4000 --space 2000 --binary-raw 8 -f monoshort.wav 500
### CARRIER 500 @ 4000.0 Hz ###
...(lots of lead-in 1s)...
11111111
11111111
11111111
10111010
00001111
10000010
...(rest of desired data)...
### NOCARRIER ndata=157 confidence=230.542 ampl=0.126 bps=499.55 (0.1% slow) ###
I
underlined what would be the data bytes for a start bit an periodicity
of 8 bits. Instead of my underlines, minimodem can actually
interpret the start bits, and print out the 7 data LSB bits of each
byte.
root@kali:~# minimodem --rx -R 44100 --mark 4000 --space 2000 --binary-output -7 --startbits 1 --stopbits 0 -f monoshort.wav 500
### CARRIER 500 @ 4000.0 Hz ###
1110100
0011111
0000100
...(remainder of desired data)...
### NOCARRIER ndata=78 confidence=62.198 ampl=0.119 bps=495.83 (0.8% slow) ###
Looking
at the hex equivalents, we get the data below. Sadly, it doesn't
look recognizable. The confidence level of the de-encoding
drops significantly from 230 down to only 62 when I forced minimodem to
look for 7N1 encoding.
root@kali:~# minimodem --rx -R 44100 --mark 4000 --space 2000 -7 --startbits 1 --stopbits 0 -f monoshort.wav 500 | xxd
### CARRIER 500 @ 4000.0 Hz ###
00000000: 177c 107c 107c 107c 107c 107c 107c 107c .|.|.|.|.|.|.|.|
00000010: 5511 7d10 0c52 5056 3f2a 0675 102c 2203 U.}..RPV?*.u.,".
00000020: 3a57 2339 6a2a 5620 132c 3129 2745 500f :W#9j*V .,1)'EP.
00000030: 0211 1f34 6b3d 2a07 7510 2661 5056 392a ...4k=*.u.&aPV9*
### NOCARRIER ndata=78 confidence=62.198 ampl=0.119 bps=495.83 (0.8% slow) ###
Then analyzing the same audio from the longer orginal file makes me
less confident:
root@kali:~# minimodem --rx -R 44100 --mark 4000 --space 2000 -7 --startbits 1 --stopbits 0 -f mono.wav 500 | xxd
### CARRIER 500 @ 4000.0 Hz ###
00000000: 2b71 4017 7c10 7c10 7c10 7c10 7c10 7c10 +q@.|.|.|.|.|.|.
00000010: 7c10 7c55 117d 100c 5250 563f 2a06 7510 |.|U.}..RPV?*.u.
00000020: 1651 1057 352a 3775 542c 3002 5d4c 6a53 .Q.W5*7uT,0.]LjS
00000030: 0c75 1016 7950 563d 2a07 7510 4c42 5056 .u..yPV=*.u.LBPV
00000040: 392a 0775 106c 1250 461a 1503 3d5f 5f58 9*.u.l.PF...=__X
### NOCARRIER ndata=77 confidence=74.856 ampl=0.120 bps=495.45 (0.9% slow) ###
It's strange
to me that when I demodulate the full-length
file, there are 3 extra bytes (probably from noise at the beginning of
the wav file that are cut out of the short version). But then the
byte sequence drops in and out of matching, then has extra bytes at the
end. I
also did not show when the long file looses carrier and then finds the
carrier again and adds on more bytes at the end because you can
obviously see
the ending noise in the spectrogram. Maybe minimodem misses a
start bits somewhere? I'm interpreting 7N1 wrong? I need
to
investigate further why the audio tracks give different bytes.
Audacity shows 1.363
seconds of data including the first start bit to
the last audio, or about 681 bits. 8 bits per character
(including the
start bit) should give about 85 characters. In fact, minimodem
decodes only 64 bytes from the trimmed audio file - maybe because there
are several places where long Mark
tones indicate data bytes were delayed by the computer and the marking
tone just held static.
Subtracting off about 14 bytes for the sync header, gives me only about
50 bytes decoded. That would match the program listing if the
line numbers were condensed somehow.
On-line research shows all sorts of protocols were used to record to
cassette tape. In 1975, there was an effort to stabilize on the Kansas City
Standard, but that didn't last very long. That was 8N2
format. Hmm...
I need to get a stable decode for both audio file durations, and
figure out how the program text was encoded onto the bit stream.
Or, maybe I'm barking up the wrong tree trying to interpret the data
with an asynchronous protocol. Cassette tapes (which this audio
was meant for) were notoriously "wobbly" so it's very believable that
Sharp used a synchronous protocol with embedded clock signals.
Guessing at synchronous protocols
With NRZS (0=transition, 1=no transition, see Wikipedia)
alternating blocks of 6 0s then 6 1s would be de-encoded as a string of
uninterrupted 1s, HDLC (after 5 bits) bit stuffing was used.
root@kali:/mnt/hgfs/xfersync-vm# minimodem --rx -R 44100 --mark 4000 --space 2000 --binary-raw 16 -f monoshort8008.wav 500
### CARRIER 500 @ 4000.0 Hz ###
1111111111111111
1111111111111111
1111111111111111
1111111111111111
1111110111010000
0111110000010000
0111110000010000
0111110000010000
0111110000010000
0111110000010000
0111110000010000
0111110000010000
0111110101010111
...
After the marking tone, and 5 glitchy bits as the audio starts, we
see...
1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
5x0 1 5x0 5x1
0101010 9x1...
So there is a pretty powerful 5-bit
sync pattern, but that would mean an NRZI lay over a "stuff a bit after
4 bit" protocol, and I don't know of any like that, and the it's not
quite alternating blocks anyhow.
Back to asynchronous protocols
Notice the raw binary (including protocol bits) with
minimodem. The "body" of the message clearly has, after the 5-bit
sync patterns, a 13-bit
pattern.
Notice the vertical columns of 1s and 0s when printed 26 bits on a line
and ignore the colored fonts and underscores which are referenced later.
root@kali:~# minimodem --rx -R 44100 --mark 4000 --space 2000 --binary-raw 26 -f monoshort8008.wav 500
### CARRIER 500 @ 4000.0 Hz ###
11111111111111111111111111
11111111111111111111111111
11111111111111111110111010
00001111100000100000111110
00001000001111100000100000
11111000001000001111100000
10000011111000001000001111
10000010000011111010101011
11111110100010001011111000
00100000110000010010111000
00101100110101110111111000
10101000110000010101111000
00100000110100010001011000
00100101110101110101011000
10101001110110010101111000
10101000110101110000011011
00100000110101110100011001
00101011110110010100011000
00101011110000010000011010
00100111110000010110011010
11101011110001010100111000
00101011110000010000011001
00100001110000010110011010
11101001110001010100111000
00101011110000010000011011
00100100110000010110011000
11100010110001010100011000
00101011110111110111111011
11101111110000110111011110
### NOCARRIER ndata=29 confidence=150.653 ampl=0.126 bps=500.04 (0.0% fast) ###### CARRIER 500 @ 4000.0 Hz ###
The 13-bit pattern can be broken down more to see a meaningful pattern:
1234567890123
110xxxx10xxxx
Minimodem can demodulates this same raw data as "Bell202-style at 500
bps":
root@kali:~/xfersync-to-host# minimodem --rx -R 44100 --mark 4000 --space 2000 --binary-output -f monoshort8008.wav 500
### CARRIER 500 @ 4000.0 Hz ###
10000011
00001111
00001111
00001111
00001111
00001111
00001111
00001111
10101011
10001000
00001001
01101011
00001010
10001000
11101011
10011101
01010111
00110101
00001101
01000001
11101000
01001010
01010001
00001010
10001001
01101011
00001010
00001100
01000011
01101011
00001010
00001101
01001001
00100001
00001010
11111011
11111011
00011011
### NOCARRIER ndata=38 confidence=25.349 ampl=0.116 bps=493.64 (1.3% slow) ###
The underscore lines and colored bits above and below seem to correlate
when interpreted as 8N1 protocol. But raw data shows 8 0xf0 while
demodulated data shows only 7 0xf0, so something still isn't
right. Maybe minimodem misses the first 0xf0 because it gets
tripped up trying to interpret that first 0 in the raw data as a start
bit and by the time it discovers there's an error (no stop bit), it's
already "cut into" the first 0xf0 byte.
In ASCII mode the 38 bytes look like this:
root@kali:~/xfersync-to-host# minimodem --rx -R 44100 --mark 4000 --space 2000 -f monoshort8008.wav 500 | xxd
### CARRIER 500 @ 4000.0 Hz ###
00000000: c1f0 f0f0 f0f0 f0f0 d511 90d6 5011 d7b9 ............P...
00000010: eaac b082 1752 8a50 91d6 5030 c2d6 50b0 .....R.P..P0..P.
00000020: 9284 50df dfd8 ..P...
### NOCARRIER ndata=38 confidence=25.349 ampl=0.116 bps=493.64 (1.3% slow) ###
In order to make sure I undertsood what minimodem is doing, I used it
to generate some tones instead of interpreting
them. Then I used Audacity to record what minimodem sent.
Contrary to several web sources, Bell 202
seems to mandate only the FSK nature of the signal and does not specify
how the raw data is encoded
into a bit stream. Minimodem sent 2 bits of mark tone, then 8N1
data, then 2 bits of mark
tone. For example, U is
really recognizable on an oscilloscope or Audacity screen. U = 55
ASII = 0101.0101 binary (remembering LSB is sent first).
Transmission starts with a marking tone, space is used for a start bit
(shown as a 0) and mark is used for a stop bit (shown as 1). For data
1=mark tone. There is also a trailing 0x0A (LF character) as an
artifact of how minimodem accepts console input on a Linux computer.
Bottom line: Minimodem does Bell202 as NRZ encoding
and does not do NRZI
encoding as part of the Bell202 implementation. The audio from my
old Sharp calculator can be interpreted as 8N1 data, but that gives
unintelligible byte sequences and has many improperly framed bits
(0data1) that minimodem overlooks or discards. That's
represented by a confidence of 150.653 demodulating the bits, but then
a only a confidence of 25.349 when un-encoding the digital data.
I still need to find the encoding done by the Sharp calculator.
It still seems important
that a 13-bit pattern follows through 100% of the data - I don't know
of any asynchronous protocol with that repeat period.
Run Length Limited methods
It may be RLL encoded, and there are many different RLL methods.
These methods use essentially lookup tables to craft special output bit
sequences for certain input bit sequences. On StackExchange for
Signal Processing, Andy viewed the raw data this way:
11111111111111
11111111111111
11111111111111
11111111111111
11111111111111
10 1110 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 0000 10 0000 1111
10 1010 10 1111 1111
10 1000 10 0010 1111
10 0000 10 0000 1
10 0000 10 0101 1
10 0000 10 1100 1
10 1011 10 1111 1
10 0010 10 1000 1
10 0000 10 1011 1
10 0000 10 0000 1
10 1000 10 0010 1
10 0000 10 0101 1
10 1011 10 1010 1
10 0010 10 1001 1
10 1100 10 1011 1
10 0010 10 1000 1
10 1011 10 0000 1
10 1100 10 0000 1
10 1011 10 1000 1
10 0100 10 1011 1
10 1100 10 1000 1
10 0000 10 1011 1
10 0000 10 0000 1
10 1000 10 0111 1
10 0000 10 1100 1
10 1011 10 1011 1
10 0010 10 1001 1
10 0000 10 1011 1
10 0000 10 0000 1
10 0100 10 0001 1
10 0000 10 1100 1
10 1011 10 1001 1
10 0010 10 1001 1
10 0000 10 1011 1
10 0000 10 0000 1
10 1100 10 0100 1
10 0000 10 1100 1
10 0011 10 0010 1
10 0010 10 1000 1
10 0000 10 1011 1
10 1111 10 1111 1
10 1111 10 1111 1
10 0001 10 1110 111
10
The pairs of 4-bit nibbles could be RLL encoded.
Solution
I started this project in 2013 and just now learned that others posted
a solution several years ago.
Look specifically at the Windows Pocket-Tools 2.01a wav2bin and bin2wav
tools. A newer
version 2.1 was created as recently as January 2020 by Torsten Mücker. Software worked great "out of the
box".
C:\Users\Dell\xfersync-vm>wav2bin.exe -p1403 monolongn3.wav basic.txt
Wave file was not normalized. wav2bin pre-amplify with factor 2 internally
Synchronisation 4009 Hz with a length of 8.0 sec found up to 8.15152 s
Pocket Computer format : 0x70 -> Basic, New
Save name :
Output format : UTF-8
Total bytes read (without header and sums): 39 until 9.514 s
The only tricky part was their software needed the full 8 second
lead-in of 4KHz to synchronize instead of my trimmed audio file.
Looking at the source-code, it appears Sharp used a heavily optimized
RLL format and tokenization of the BASIC programs to make really
concise audio files.
If Audicaty is used to normalize the wave file to -3dB, the program
does not have to internally normalize it. In this specific case,
there is a large amplitude spike at the beginning of the full-length
file that tricks Audacity, so normalizing to -2dB is required to get
rid of the warning message. The program read the wave file and
popped a text version of the original BASIC program out onto my hard
drive.
C:\Users\Dell\xfersync-vm>type basic.txt
10 INPUT A
20 FOR I=A TO 0 STEP -1
30 PAUSE I
40 NEXT I
50 BEEP A
Thank you :-) If you're interested in these older Sharp pocket
computers, visit the two websites linked above! They also have a
number of other related tools posted.
Summary
This calculator is a fully functional BASIC interpreter is
running on a 1980s
era handheld calculator, running on two little batteries that last for years.
My personal experience was coming back to the computer 7 years after
writing the program above and the batteries were still good. This
makes me
think of all sorts of remote automation ideas. This
could be a supervisory computer that monitor mechanical health and
welfare of a remote cottage or machine or radio station or
whatnot. Because it needs no external power for years,
it can monitor the health of other, more capable, control systems that
need power and are liable to malfunction with power loss.
The problem with this calculator is that when
batteries are changed, you
lose all the memory on the calculator. I can save
programs and memory variables to my desktop in the form of audio
files.
If I can interpet the audio, I'll have a way to create programs on a
desktop and run them on the calculator. The next project is to write an
"audio cross-compiler" that can take a BASIC
program from other sources and modulate it into a wav file, which can
then be uploaded to the Sharp EL-5500. If you want to collaborate on
making this happen, please contact me.
Additional Resources
- HP-20S on Wikipedia
(public authors)
- EL-5500 on
promsoft.com
- EL-5500
Operation Manual (more pages as I have time)
- https://www.hpmuseum.org/forum/thread-7604.html
- https://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/archv017.cgi?read=110792#111281
- https://www.hpmuseum.org/cgi-sys/cgiwrap/hpmuseum/archv017.cgi?read=110792#111389
- https://edspi31415.blogspot.com/2018/05/fun-with-sharp-el-5500-iii-may-2018.html
- https://www.calculator.org/calculators/Sharp_EL-5500.html
- http://www.leucht.com/blog/2013/06/my-pocket-computer-from-high-school-sharp-el-5500-iii
The
skeleton of this document was originally created using AbiWord
under a Gnome desktop. It was subsequently edited by Konquerer to
become the web page you are reading. Created March 2013. Last
updated November 2020.
